👉NCERT SOLUTIONS FOR CLASS 10 MATHS CHAPTER 3 PAIR OF LINEAR EQUATION IN TWO VARIABLE EX 3.2
👉 EXERCISE 3.2 CLASS 10 MATHS
👉 NCERT SOLUTIONS FOR CLASS 10 MATHS EXERCISE 3.2 CHAPTER 3
इस ब्लॉग में में आपको NCERT SOLUTIONS FOR CLASS 10 MATHS CHAPTER 3 PAIR OF LINEAR EQUATION IN TWO VARIABLE EX 3.2 को detail में समझाऊंगा।
प्रश्न -(1) निम्न समस्याओ में रेखिक समीकरणों के युग्म बनाइये और उनके ग्राफीय विधि से हल ज्ञात कीजिये :
(1) कक्षा X के 10 विद्यार्थियों ने एक गणित की पहली प्रतियोगिता में भाग लिया। यदि लड़कियों की संख्या लड़को की संख्या से 4 अधिक हो तो प्रतियोगिता में भाग लिए लड़को और लड़कियों की संख्या ज्ञात कीजिये।
(II ) 5 पेंसिल तथा 7 कलमों का कुल मूल्य 50 रुपये हे जबकि 7 पेंसिल तथा 5 कलमों का मूल्य 46 रुपये एक पेंसिल का मूल्य तथा एक कलम का मूल्य ज्ञात कीजिये।
हल : (I) मान लीजिये प्रतियोगिता में भाग लेने वाले लड़को एवं लड़कियों की संख्या क्रमशः X और Y हे
तब प्रश्नानुसार , X + Y = 10 --------->(1)
Y = 10 - X
एवं Y = X + 4 ---------> (2)

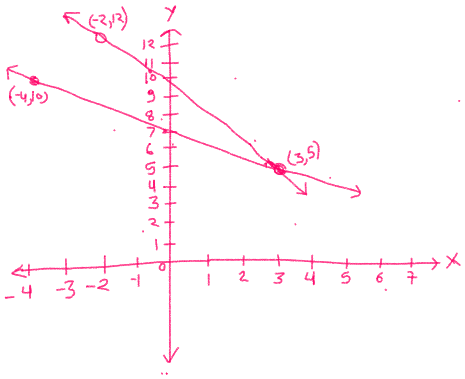
दोनों ग्राफ परस्पर बिन्दू P ( 3 ,7 ) पर प्रतिच्छेद करते हे। अतः लड़के एवं लड़कियों की संख्या क्रमशः
3 एवं 7 हे।
(ii) मानलो पेंसिल और कलम का मूल्य क्रमशः x रुपये प्रति नग एवं y रुपये प्रति नग हे।
तो प्रश्नानुसार ,
5x + 7y = 50 --------> (1 )
y = (50 - 5x ) / 7
एवं 7 x + 5 y = 46 ---------> (2 )
y =( 46 - 7x ) / 5
चूँकि दोनों ग्राफ (3 , 5 ) पर परस्पर प्रतिच्छेद करते हे। अतः पेंसिल एवं कलम 3 रुपये प्रति नग एवं 5 रुपये प्रति नग हे।
ENGLISH TRANSLATION :
Question - (1) Form the pair of linear equations in the following problems and find their solution by graphical method :
(1) 10 students of class X participated in the first math competition. If the number of girls is 4 more than the number of boys, then find the number of boys and girls who participated in the competition.
(II) The total cost of 5 pencils and 7 pens is R s 50 while the cost of 7 pencils and 5 pens is Rs 46. Find the cost of one pencil and the cost of one pen.
Solution : (I) Let the number of boys and girls participating in the competition be X and Y respectively.
Then according to the question, X + Y = 10 --------->(1)
Y = 10 - X
and Y = X + 4 ---------> (2)
Both the graphs intersect each other at the point P ( 3 , 7 ). Hence the number of boys and girls respectively 3 and 7
(ii) Let the cost of pencil and pen be R s. x per piece and R s. y per piece respectively.
So according to the question,
5x + 7y = 50 --------> (1)
y = (50 - 5x ) / 7
and 7 x + 5 y = 46 ---------> (2)
y =( 46 - 7x ) / 5
Since both intersect each other on the graph (3 , 5 ). Hence pencil and pen are Rs.3 per piece and Rs.5 per piece.
प्रश्न -(2) अनुपातों a 1 / a 2 , b 1 / b 2 और c 1 / c 2 की तुलना कर ज्ञात कीजिये की निम्न समीकरण युग्म द्वारा निरूपित रेखाएं एक बिंदु पर प्रतिच्छेद करती हे , समानांतर हे अथवा सम्पाती हे।
(i) 5x -4y +8 = 0 (ii) 9x + 3y +12 = 0 (iii) 6x - 3y +10 = 0
7x +6y -9 = 0 18x + 6y +24 = 0 2x -y + 9 = 0
हल : चूँकि 5x -4y +8 = 0
एवं 7x +6y -9 = 0
यहाँ दिए गए समीकरण की तुलना a 1 x + b 1 y + c 1 = 0 तथा a 2 x + b 2 y + c 2 = 0 से करने पर ,
a 1 = 5 , b 1 = -4 , c 1 = 8
तथा a 2 = 7 , b 2 = 6 , c 2 = -9
इसलिए , a 1 / a 2 = 5 / 7 , b 1 / b 2 = -4 / 6 , c 1 / c 2 = 8 / -9 = -8 / 9
स्पष्ट हे की , a 1 / a 2 बराबर नहीं , b 1 / b 2 बराबर नहीं c 1 / c 2 के।
अतः रेखाएं एक बिंदु पर प्रतिच्छेद करती हे। अतः समीकरण निकाय का अद्वितीय हल होगा।
(ii) 9x + 3y +12 = 0
18x + 6y +24 = 0
हल : इस समीकरण की तुलना सामान्य समीकरण a 1 x + b 1 y + c 1 = 0 तथा a 2 x + b 2 y + c 2 = 0 से करने पर ,
a 1 = 9 , b 1 = 3 , c 1 = 12
तथा a 2 = 18 , b 2 = 6 , c 2 = 24
इसलिए , a 1 / a 2 = 9 / 18 = 1 / 2 , b 1 / b 2 = 3 / 6 = 1 / 2 , c 1 / c 2 = 12 / 24 = 1 / 2
यहाँ स्पष्ट हे की , a 1 / a 2 = b 1 / b 2 = c 1 / c 2
अतः समीकरण युग्म द्वारा निरूपित रेखाएं सम्पाती हे।
(iii) 6x - 3y +10 = 0
2x -y + 9 = 0
हल : इस समीकरण की तुलना सामान्य समीकरण a 1 x + b 1 y + c 1 = 0 तथा a 2 x + b 2 y + c 2 = 0 से करने पर ,
a 1 = 6 , b 1 = -3 , c 1 = 10
तथा a 2 = 2 , b 2 = -1 , c 2 = 9
इसलिए a 1 / a 2 = 6 / 2 = 3 / 1 , b 1 / b 2 = -3 / -1 = 3 / 1 , c 1 / c 2 = 10 / 9
स्पष्ट हे की , a 1 / a 2 बराबर हे b 1 / b 2 के , लेकिन c 1 / c 2 के बराबर नहीं हे।
अतः समीकरण युग्म द्वारा निरूपित रेखाएं समांतर हे।
ENGLISH TRANSLATION :
Question -(2) By comparing the ratios a 1 / a 2 , b 1 / b 2 and c 1 / c 2, find whether the lines represented by the following pair of equations intersect at a point, are parallel or coincide.
(i) 5x -4y +8 = 0 (ii) 9x + 3y +12 = 0 (iii) 6x - 3y +10 = 0
7x +6y -9 = 0 18x + 6y +24 = 0 2x -y + 9 = 0
Solution : Since 5x -4y +8 = 0
and 7x +6y -9 = 0
Here, comparing the given equation with a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0,
a 1 = 5 , b 1 = -4 , c 1 = 8
and a 2 = 7 , b 2 = 6 , c 2 = -9
Therefore, a 1 / a 2 = 5 / 7 , b 1 / b 2 = -4 / 6 , c 1 / c 2 = 8 / -9 = -8 / 9
Clearly, a 1 / a 2 is not equal, b 1 / b 2 is not equal to c 1 / c 2.
Hence the lines intersect at a point. Hence, the system of equations will have a unique solution.
(ii) 9x + 3y +12 = 0
18x + 6y +24 = 0
Solution : Comparing this equation with the general equation a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0,
a 1 = 9 , b 1 = 3 , c 1 = 12
and a 2 = 18 , b 2 = 6 , c 2 = 24
Therefore, a 1 / a 2 = 9 / 18 = 1/2 , b 1 / b 2 = 3 / 6 = 1/2 , c 1 / c 2 = 12 / 24 = 1/2
Here it is clear that a 1 / a 2 = b 1 / b 2 = c 1 / c 2
So the lines represented by the pair of equations coincide.
(iii) 6x - 3y +10 = 0
2x -y + 9 = 0
Solution : Comparing this equation with the general equation a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0,
a 1 = 6 , b 1 = -3 , c 1 = 10
and a 2 = 2 , b 2 = -1 , c 2 = 9
Therefore a 1 / a 2 = 6 / 2 = 3 / 1 , b 1 / b 2 = -3 / -1 = 3 / 1 , c 1 / c 2 = 10 / 9
Obviously, a 1 / a 2 is equal to b 1 / b 2 , but c 1 / c 2 is not equal.
So the lines represented by the pair of equations are parallel.
प्रश्न -(4) निम्न रेखिक समीकरणों के युग्मो में से कोन से युग्म संगत या असंगत हे। यदि संगत हे तो ग्राफीय विधि से हल कीजिये।
(i) x + y = 5 ; 2x + 2y = 10
(ii) x - y = 8 ; 3x - 3y = 16
(iii) 2x + y - 6 ; 4x -2y - 4 = 0
(iv) 2x - 2y -2 = 0 ; 4x - 4y - 5 = 0
हल : (i) x + y = 5 => x + y - 5 = 0 ---------> (1)
2x + 2y = 10 => 2x + 2y - 10 = 0 --------> (2)
इस समीकरण की तुलना सामान्य समीकरण a 1 x + b 1 y + c 1 = 0 तथा a 2 x + b 2 y + c 2 = 0 से करने पर ,
a 1 = 1 , b 1 = 1 , c 1 = -5
a 2 = 2 , b 2 = 2 , c 2 = -10
अतः उक्त रैखिक समिकरणो के युग्म संगत हे। रैखिक समीकरण युग्म का ग्राफीय हल हे।
चूँकि x + y = 5
y = 5 - x ------- ( 3 )
x = 0 रखने पर ,
y = 5 - 0
y = 5
x = 5 समीकरण ( 3 ) में रखने पर ,
y = 5 - 5 =0
तथा 2x + 2y = 10
y = (10 - 2x) / 2 ------- ( 4 )
x = 0 रखने पर ,
y = (10 - 2 * 0 ) / 2
y = 10 / 2
y = 5
x = 5 रखने पर ,
y = (10 - 2 * 5 ) / 2
y = (10 - 10) / 2
y = 0 / 2
y = 0
चूँकि रेखा युग्म सम्पाती हे , इसलिए रेखा का प्रत्येक बिंदु इसका हल होगा। अतः उक्त रैखिक समीकरण अनंत अनेक हल होंगे।
(ii) चूँकि x - y = 8 => x - y - 8 = 0 ---------> ( 1 )
एवं 3 x - 3y = 16 => 3x - 3y -16 = 0 -------> ( 2 )
इसलिए ,
उक्त रेखिक समीकरण का युग्म असंगत हे।
(iii ) चूँकि 2x + y -6 = 0 ---------> ( 1 )
4x -2y -4 = 0 ---------- > ( 2 )
उक्त रेखिक समीकरण के युग्म संगत हे। रेखीय समीकरण युग्म का ग्राफीय हल :
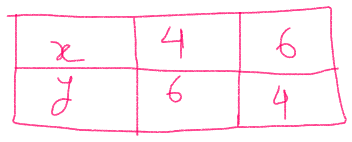
चूँकि , 2x + y -6 = 0
y = 6 - 2x -----(3 )
x = 0 रखने पर ,
y = 6 - 2 * 0
y = 6
पुनः x = 3 रखने पर ,
y = 6 - 2 * 3
y = 6 - 6
y = 0
एवं 4x -2y -4 = 0
y = 2x - 2 -------> (4 )
x = 1 रखने पर ,
y = 2 * 1 -2
y = 2 - 2 = 0
x = 4 रखने पर ,
y = 2 * 4 - 2
y = 8 - 2
y = 6

उक्त रेखिक समीकरण का हल (2 , 2 ) अर्थात x = 2 , y = 2
(iv) चूँकि 2x - 2y -2 =0 -------- > ( 1 )
एवं 4x -4y -5 =0 --------- > (2 )
अतः उक्त रैखिक समीकरण युग्म असंगत हे। अर्थात रेखा युग्म समांतर हे।
Question-(4) Which of the following pairs of linear equations is compatible or inconsistent with? If relevant, solve by graphical method.
(i) x + y = 5 ; 2x + 2y = 10
(ii) x – y = 8 ; 3x - 3y = 16
(iii) 2x + y – 6 ; 4x -2y - 4 = 0
(iv) 2x – 2y – 2 = 0 ; 4x - 4y - 5 = 0
Solution : (i) x + y = 5 => x + y - 5 = 0 ---------> (1)
2x + 2y = 10 => 2x + 2y - 10 = 0 --------> (2)
Comparing this equation with the general equations a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0,
a 1 = 1 , b 1 = 1 , c 1 = -5
a 2 = 2 , b 2 = 2 , c 2 = -10
Hence, the above pair of linear equations are compatible. is the graphical solution of a pair of linear equations.
Since x + y = 5
y = 5 - x ------- ( 3 )
Keeping x = 0,
y = 5 - 0
y = 5
Substituting x = 5 in equation ( 3 ) ,
y = 5 - 5 =0
and 2x + 2y = 10
y = (10 - 2x) / 2 ------- ( 4 )
Keeping x = 0,
y = (10 - 2 * 0 ) / 2
y = 10 / 2
y = 5
Keeping x = 5,
y = (10 - 2 * 5 ) / 2
y = (10 - 10) / 2
y = 0 / 2
y = 0
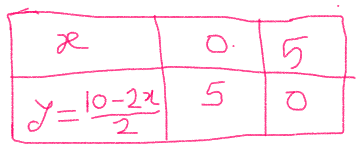

Since the pair of lines coincide, every point on the line will be its solution. Hence, the above linear equation will have infinitely many solutions.
(ii) Since x - y = 8 => x - y - 8 = 0 ---------> ( 1 )
and 3 x - 3y = 16 => 3x - 3y -16 = 0 -------> ( 2 )
Therefore ,

The pair of the above linear equation is inconsistent.
(iii) Since 2x + y -6 = 0 ---------> ( 1 )
4x -2y -4 = 0 ---------- > ( 2 )
The pairs of the above linear equation are compatible. Graphical Solution of a Pair of Linear Equations:
Since , 2x + y -6 = 0
y = 6 - 2x -----(3 )
Keeping x = 0,
y = 6 - 2 * 0
y = 6
Putting again x = 3,
y = 6 - 2 * 3
y = 6 - 6
y = 0
and 4x -2y -4 = 0
y = 2x - 2 -------> (4)
Putting x = 1,
y = 2 * 1 -2
y = 2 - 2 = 0
Putting x = 4,
y = 2 * 4 - 2
y = 8 - 2
y = 6
Solution of the above linear equation (2 , 2 ) i.e. x = 2 , y = 2
(iv) Since 2x - 2y -2 =0 -------- > ( 1 )
and 4x -4y -5 =0 --------- > (2 )
Hence, the above pair of linear equations is inconsistent. That is, the line pair is parallel.